pandas.Series.plot.kde

Series.plot.kde(bw_method=None, ind=None, **kwargs)

使用高斯核函数生成核密度估计图。

在统计学中，kernel density estimation (KDE) 是一种估计随机变量概率密度函数 (PDF) 的非参数方法。此函数使用高斯核函数，并包含自动带宽确定。

Parameters:

bw_methodstr，标量或可调用对象，可选

用于计算估计器带宽的方法。可以是 ‘scott’、’silverman’、一个标量常数或一个可调用对象。如果为 None (默认)，则使用 ‘scott’。有关更多信息，请参阅 scipy.stats.gaussian_kde 。

indNumPy 数组或 int，可选

用于评估估计 PDF 的点。如果为 None (默认)，则使用 1000 个等间距点。如果 ind 是 NumPy 数组，则在传入的点上评估 KDE。如果 ind 是一个整数，则使用 ind 个等间距点。

**kwargs

附加关键字参数在 DataFrame.plot() 中有详细说明。

Returns:

matplotlib.axes.Axes 或它们的 numpy.ndarray

参见

scipy.stats.gaussian_kde

使用高斯核函数进行核密度估计的表示。这是用于估计 PDF 的内部使用的函数。

Examples

给定从未知分布随机抽样的点序列，使用具有自动带宽确定的 KDE 估计其 PDF，并绘制结果，在 1000 个等间距点（默认）处进行评估：

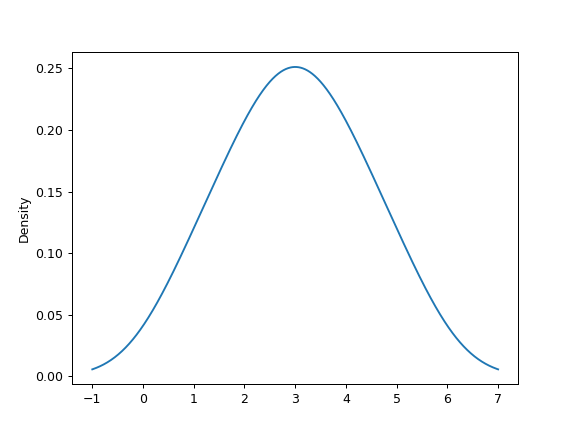
>>> s = pd.Series([1, 2, 2.5, 3, 3.5, 4, 5])
>>> ax = s.plot.kde()

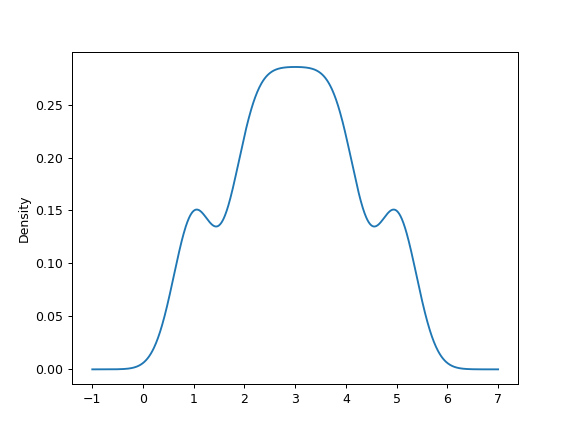
可以指定一个标量带宽。使用小的带宽值可能导致过拟合，而使用大的带宽值可能导致欠拟合：

>>> ax = s.plot.kde(bw_method=0.3)

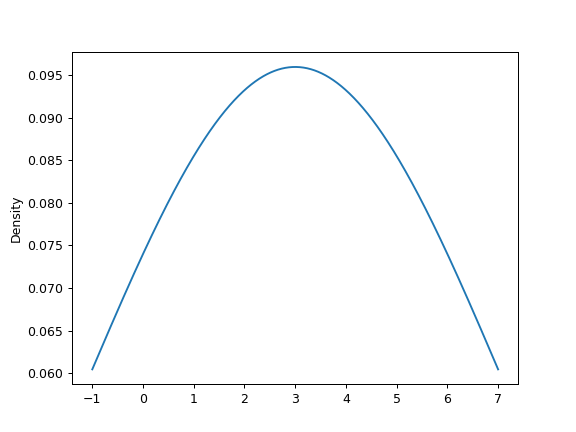
>>> ax = s.plot.kde(bw_method=3)

最后，ind 参数确定估计 PDF 图的评估点：

>>> ax = s.plot.kde(ind=[1, 2, 3, 4, 5])

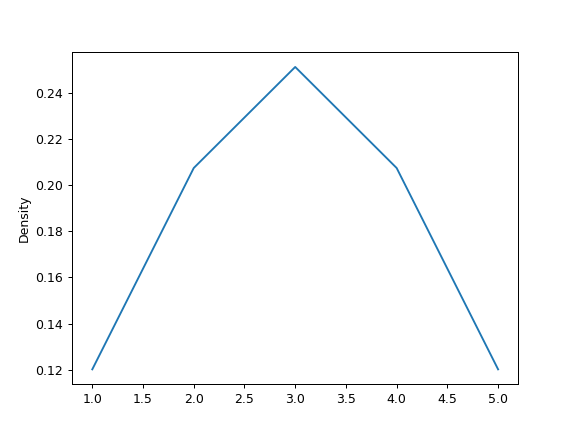
对于 DataFrame，其工作方式相同：

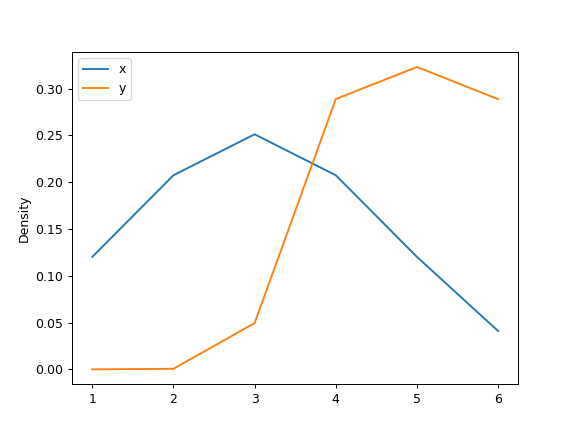
>>> df = pd.DataFrame({
...     'x': [1, 2, 2.5, 3, 3.5, 4, 5],
...     'y': [4, 4, 4.5, 5, 5.5, 6, 6],
... })
>>> ax = df.plot.kde()

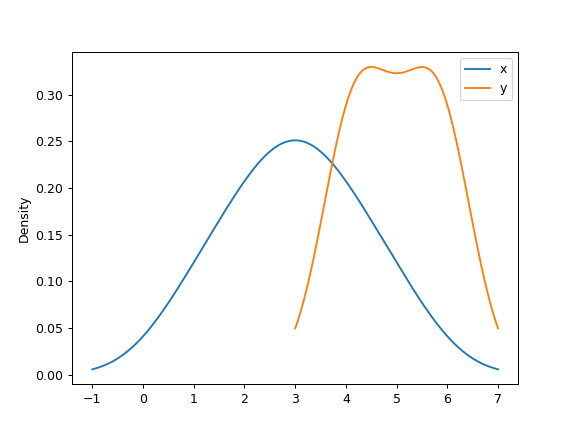
可以指定一个标量带宽。使用小的带宽值可能导致过拟合，而使用大的带宽值可能导致欠拟合：

>>> ax = df.plot.kde(bw_method=0.3)

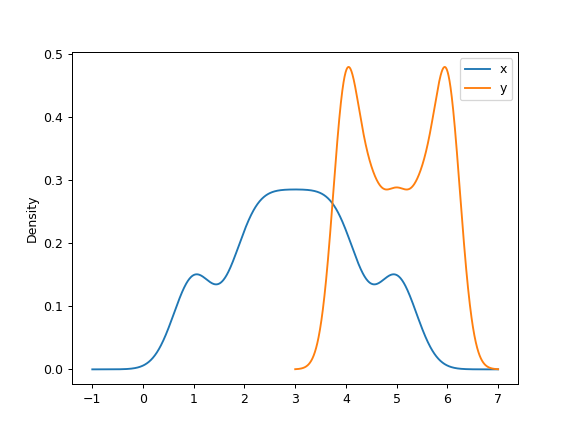
>>> ax = df.plot.kde(bw_method=3)

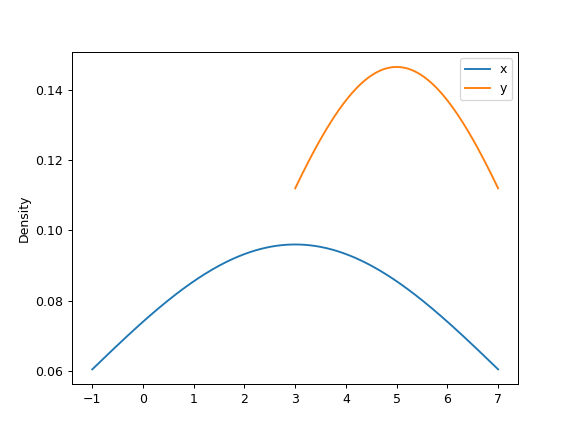
最后，ind 参数确定估计 PDF 图的评估点：

>>> ax = df.plot.kde(ind=[1, 2, 3, 4, 5, 6])